・東中3年生2学期期末テストの範囲
いよいよ彦根市立東中学校3年生の2学期期末テストが間近に迫ってきました。当塾の3年生達はほぼ毎日通塾してテスト対策の勉強を行っています。
3年生は11月12,13日と1,2年生より早く実施されます。実力テストもあるので先に行われるので、範囲が狭くなりますが内容は各科目とも難しい問題が多いです。本日は数学について解説します。

数学の範囲は上の表の様に相似が多くを占めます。また相似の面積比・体積比は範囲外です。二次関数も曲線のグラフではないので比較的簡単だと思います。難しいのはやはり証明で、中学の数学で1番難しいのは証明と言われているのでしっかり対策しないと、仮定すらわからないでしょう。ただ円周角や三平方の定理など他の単元との組み合わせの問題ではなく、三角形を使用した証明ですので教科書やワークをくり返し復習すれば理解できるはずです。
それでは細かい単元事に解説します。
・いろいろな関数
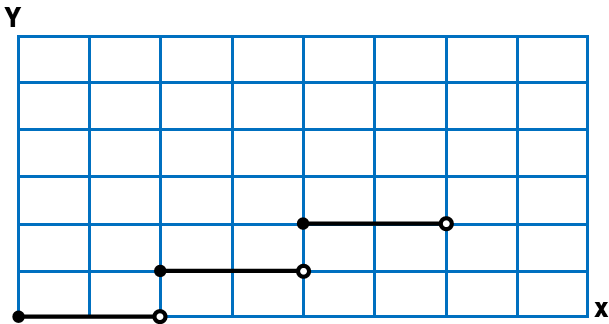
いろいろな関数は上の表の様にある範囲では値が変化しないグラフです。xが増加するとyも増加しますが、yの値はxの一定の範囲では変化しません。ポイントカードとかの問題で出題されますね。ここで注意するのは棒線の●は値を含む記号、〇はその値を含まない記号です。xの当符号をよく見て丸印を書きましょう。
・相似-拡大図、縮図
相似で最初に学ぶのは図形の拡大図、縮図です。1点を基準にして図形の頂点等に線を引いて、拡大図・縮図を作成します。こちらは比較的簡単ですので、点と頂点をずれないように描けば大丈夫です。
・相似-三角形の相似条件
三角形の必ず出題されるので、絶対に覚えましょう!語順もきちんと覚えて教科書通りに書けるよう、何回もノートに書くなどして暗記しましょう。また複数の三角形から相似な三角形を選択して、なぜ相似なのか該当する相似条件を書く問題も出題されるかもしれません。
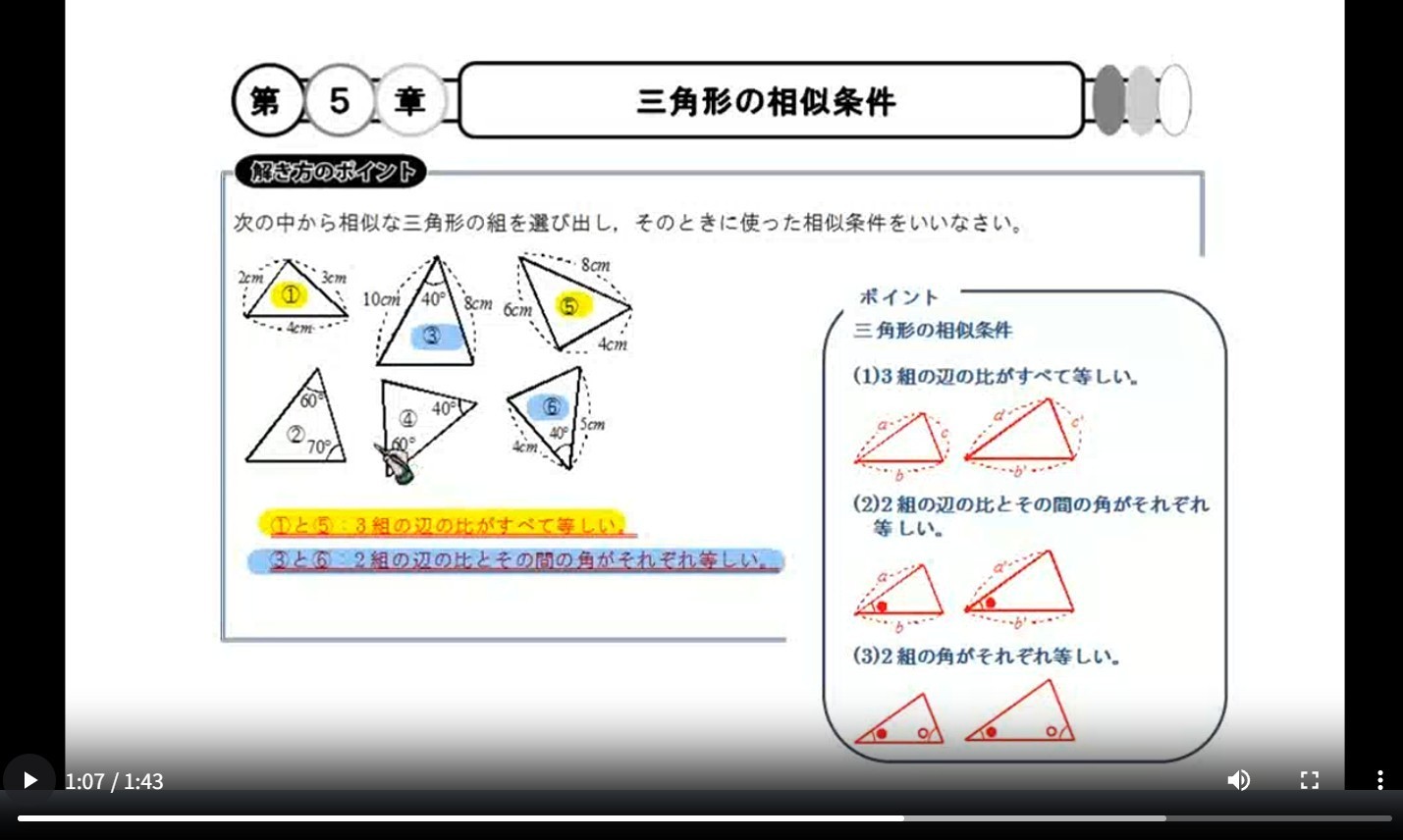
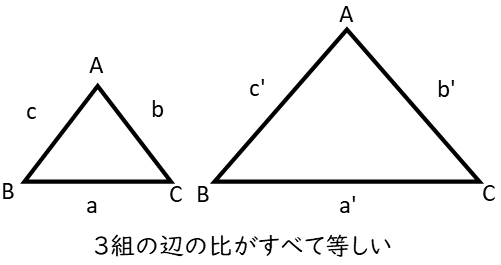
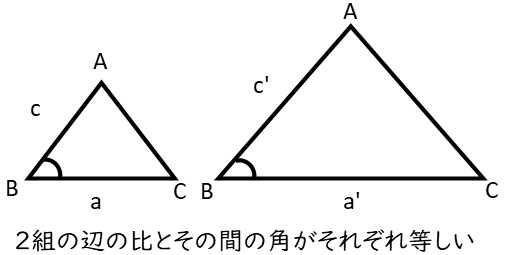
三角形の相似条件は下図の通りです。
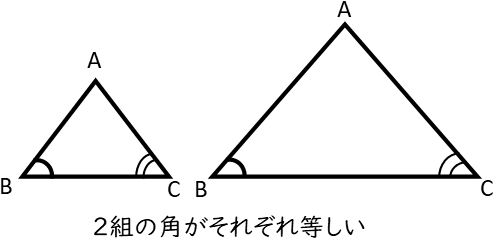
・相似-三角形の相似条件を使った証明
おそらく相似の証明問題は。穴埋め問題と全く白紙の欄に解答を記入する二問くらい出題されると思います。
穴埋め問題の注意する点は証明する2つの三角形の辺や角度を書くときは、英文字の順番に気をつけることです。
例えば△ABC∽△DEFの相似を証明する場合、辺ABに対応する辺は辺DE、∠BCAに対応する角は∠EFDと英文字の順番を同じにしましょう。対応する辺や角が合っていても英文字の順が逆だと減点する先生もおられます。
次に図形を用いて解きやすい方法を教えます。
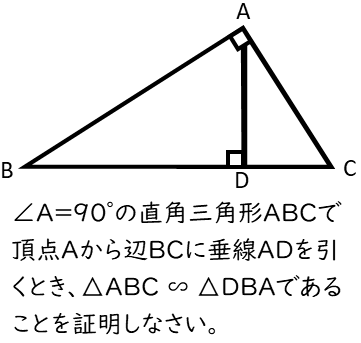
上図の問題の場合、問題の図形に直接証明に該当する辺や角に印をつけていくとややこしくなります。そこで問題用紙の空いた場所に手描きでいいので証明する三角形を描くとわかりやすくなります。
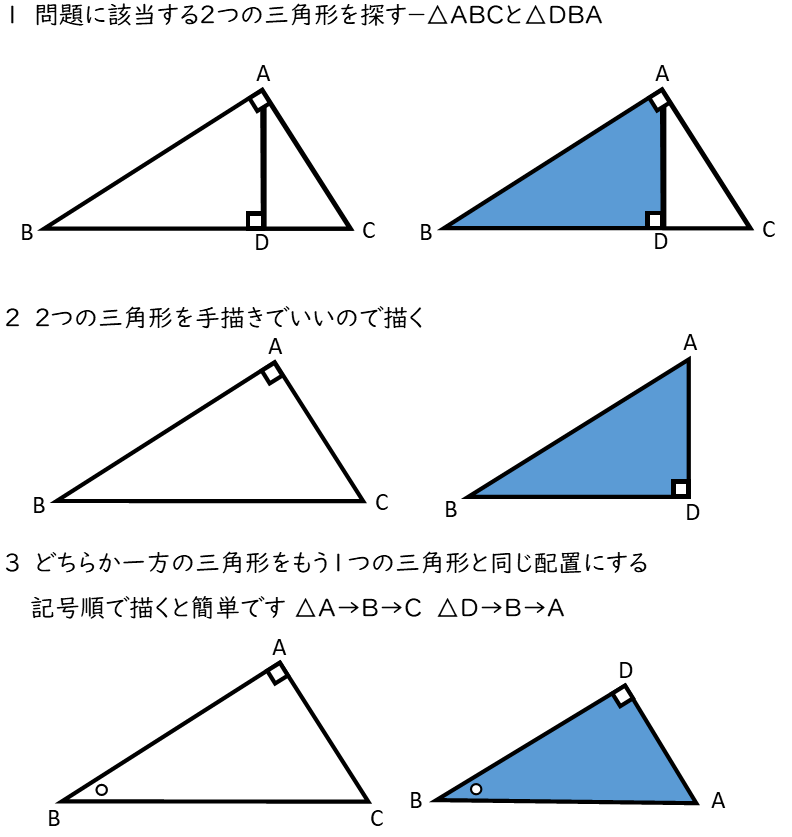
1.まず証明する三角形を探しましょう。この場合一番外側の辺で形成されている△ABCとその中にある左側の小さな△DBAになりますね。
2.次に用紙の空いたところに手描きでいいので、証明する三角形を描きます。
3.そしてどちらか一方の三角形(この場合は△DBA)を、もう一つの三角形と同じ記号順になるように描き直します。左の△ABCと似た三角形を描いて、△ABCと同じ順に英文字を書きましょう(D→B→A)。
このように描くと∠Aと∠Dが90°で同じ角度、また∠Bは重なり合った共通の角度であることがわかります。これで「2組の角度がそれぞれ等しい」という相似条件に当てはまり、△ABC ∽ △DBAとなります。
このような問題は大抵後の三角形(この場合△DBA)は対称移動と回転移動(ようはひっくり返した)している状態なので、頭の中で図形を思い浮かべても中々まとまりません。また問題用紙の三角形に対応する辺や角に直接印をつけてもどれがどれに対応しているかわかりにくくなります。ですから、自分でゆがんでいてもいいので三角形を2つ描いて問題文から比で合う辺や同じ角度を探して印をつける方が間違いにくいのですね。
手間がかかりそうですが慣れると、こちらの方が相似条件に必要な辺や角度がすぐにわかります。一度試して下さい。
・相似-相似の利用
相似の利用は木やビルの高さ、池の長さを求めるのに使われます。
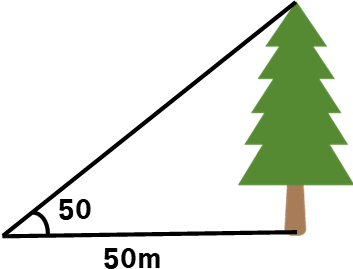
このような問題で木の高さを求めます。これらの問題は問題用紙の下の50mを定規で何cmか測り、問題用紙の長さが何分の1になっているのか求めてから計算します。ですから比の解き方 a : b = c : d で解けますし、また何分の1かわかれば定規で木の長さを測り実際の長さに計算すれば大丈夫です。
・相似-誤差
誤差の値は ( 誤差 ) = ( 近似値 ) - ( 真の値 ) で求めます。また大きな数字、1000000000000を10の累乗で表す問題も出題されます。計算は簡単でしょうが、以外と単語が問題で出るかもしれません。「誤差」「近似値」「真の値」「絶対値」「有効数字」などは覚えましょう。
・相似-平行線と線分の比
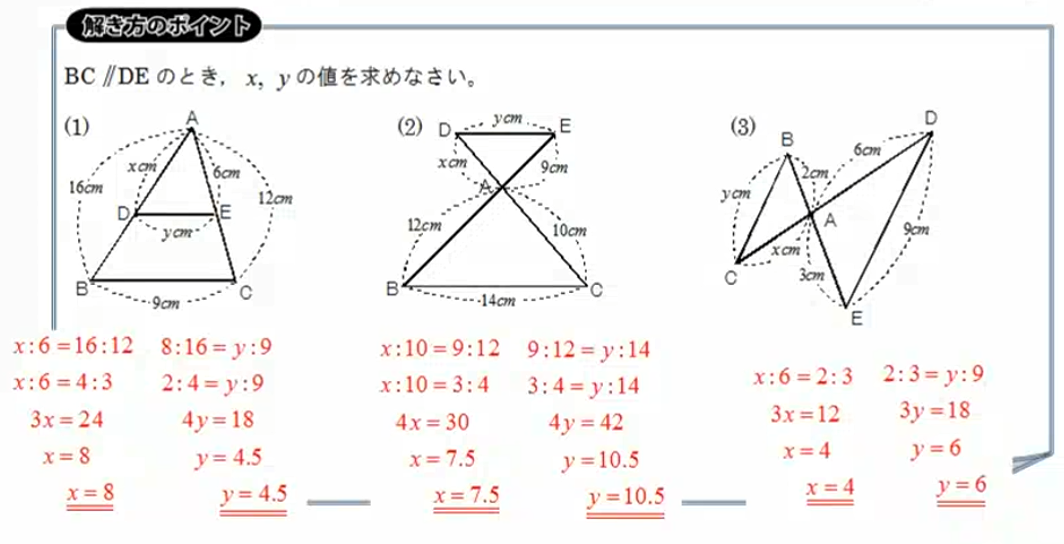
三角形の中に1つの辺に平行な線を引いて、辺の長さを求める問題です。また下図(2)(3)のように頂点がつながり、辺が平行な三角形で辺の長さを求める計算も出ます。
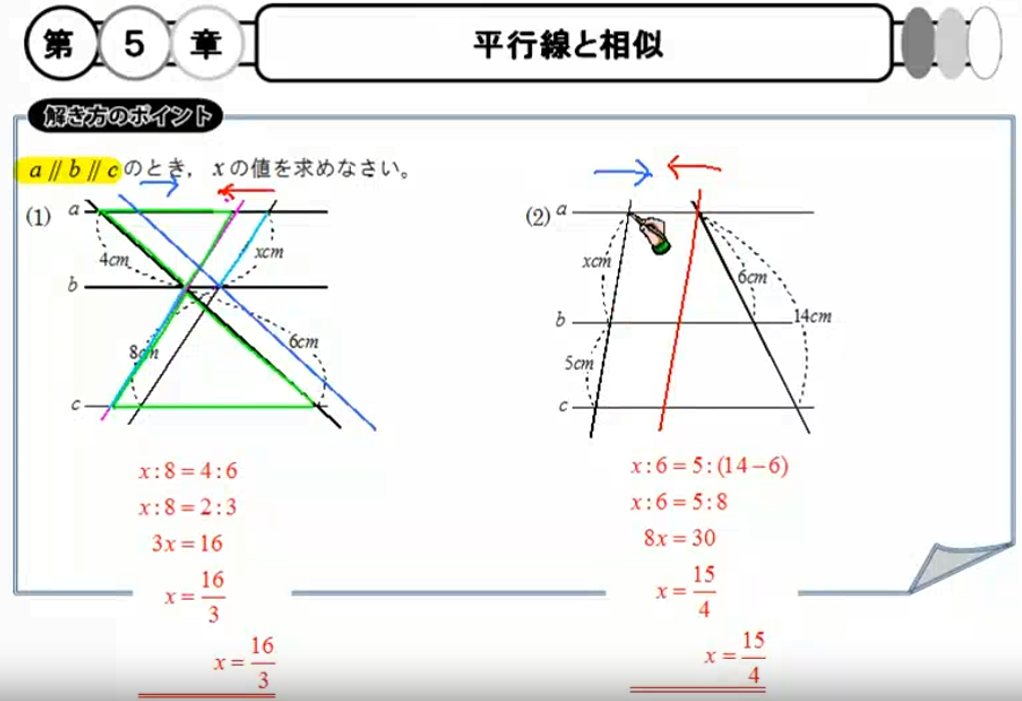
他にも下図のように平行な線分が並んでいる所に、斜めの線を描いて各辺の長さを求める計算も出題されるでしょう。この場合一方の斜めの線を移動してもう一方の斜めの線と平行な線上で交じるようにすれば簡単です。
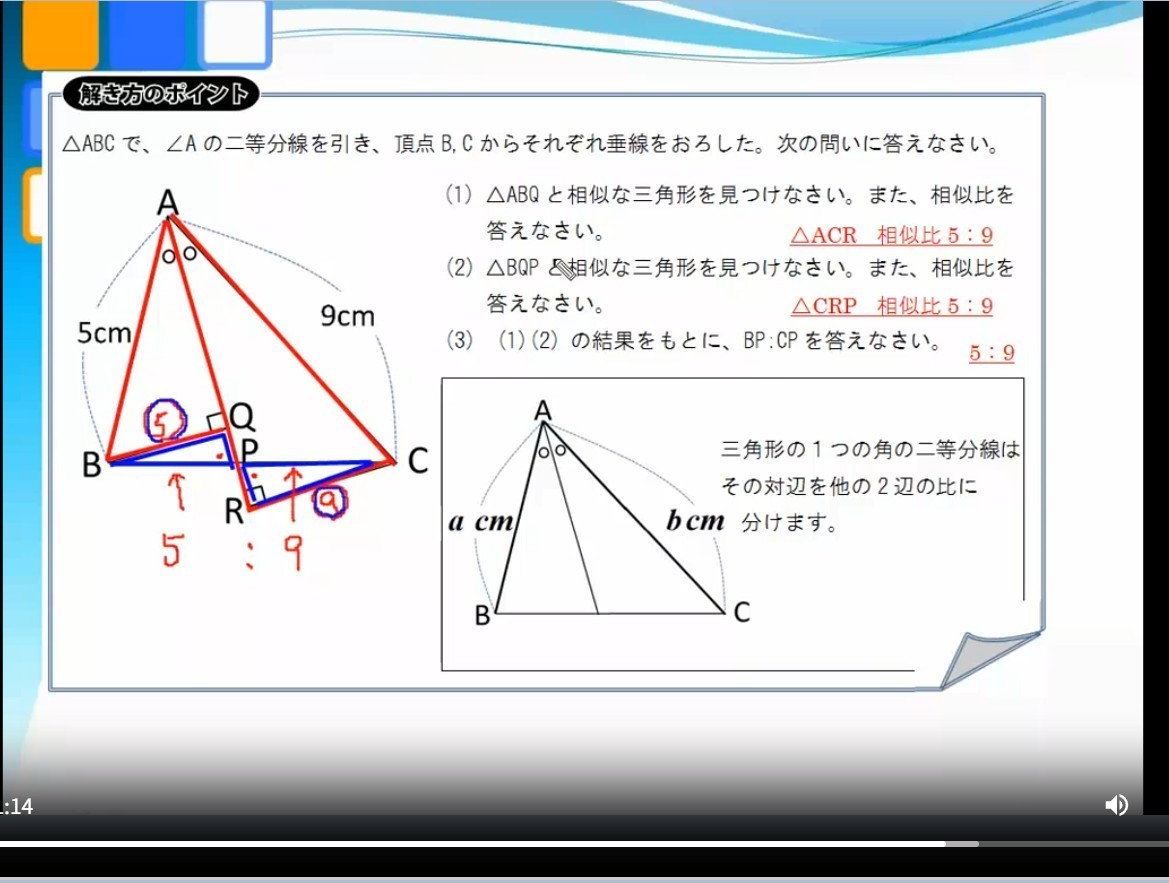
・相似-角の二等分線
角の二等分線は一つの角を二等した線とその線と交わる辺は、二等分された角に接する辺の長さに分かれるという定理です。またなぜ角の二等分線はその対辺を他の2辺の比にわけるのかの証明問題が出題されるかもしれません。
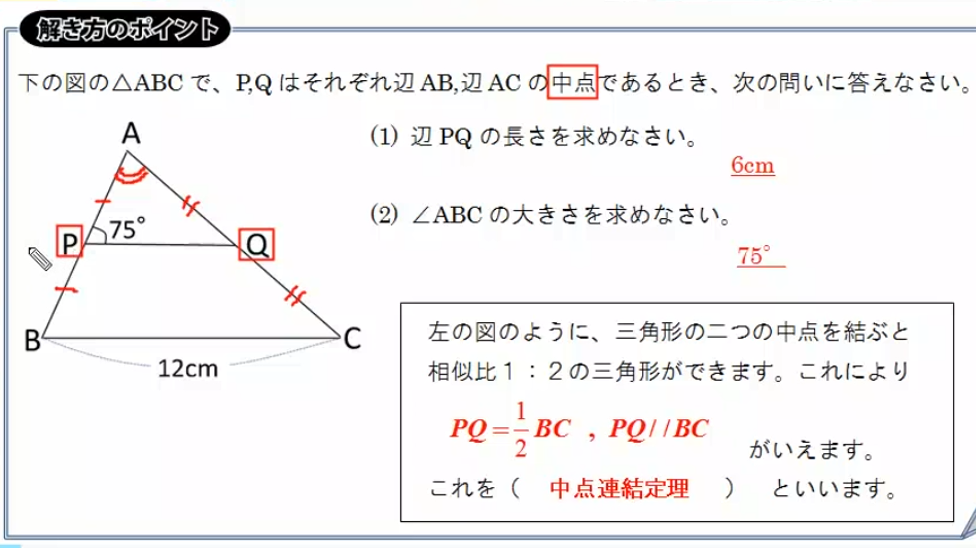
・相似-中間連結定理
中間連結定理とは三角形で、接する二辺のそれぞれの中点を結ぶとその線はもう1辺と平行になる定理です。
解き方を覚えるのも大変ですが、この定理を使って平行四辺形の証明ができます。もしかすると出題されるかもしれないので、教科書やワークで復習しましょう。
・今までの計算問題も出題されます!
範囲表には「今までに学習した計算問題は出題します」と書かれているので復習は必須です。
「多項式の計算」「因数分解」「平方根」「二次方程式」「二次関数」などから出題されるでしょう。「二次関数」もグラフは出ないでしょうがxとyの座標から y = ax の a の値を求めるような問題があるかもしれません。
・問題数が多いと予想されます
二次関数、相似に加えて今までの計算問題も出題されるので、範囲はかなり広いでしょう。時間はあとわずかですが、ワークの見直しなどで計算問題の復習をしっかりと行いましょう。相似で頑張って点数を取っても、計算問題で点数が取れないかもしれません。
後悔の無いよう勉強しましょう!
本日は以上です。
個別進学塾レッツリトライ 彦根市西沼波町98
代表 馬場 崇暢
指導対象小学校:旭森小学校、佐和山小学校、城東小学校
指導対象中学校:彦根市立東中学校、彦根市立彦根中学校、彦根市立南中学校等、彦根市内の中学校
指導対象高等学校:翔西館高校、彦根東高校、米原高校、河瀬高校等、滋賀県内の県立高校、私立高校
