小学校の算数では５年生に学ぶ【単位量あたりの大きさ】と【割合】がとても難しい学習内容になっています。どちらも小学生には一番難しいと言われており、カラーテストを対策せずに行うと５０～７０点代が多くなり、しっかり対策しないと高得点は取れません。

　計算自体は難しくないのですが、どちらをどちらで割るのかの式を作るのが間違えやすいです。「もとになる量」と「求める量」を混合しがちで、さらに百分率や歩合の問題も含まれますので覚える式も多くみなさん苦戦されます。

　当塾では映像授業で視聴して、また学校のドリル・プリントの復習で自分で式を作るように教えています。特にドリルの復習は効果的なので集中的に反復復習しています。

　割合は「比べる量　÷　もとにする量」で求められます。上図のＡチームの場合、これまでの試合数は６、そのうち勝った試合は３ですから勝った割合は、３　÷　６　で　０．５になります。

　割合は全体の中のいくらかを求める問題なので、１．０を超える答えは間違いになります。特に文章で問題が出た場合は、どちらをどちらで割るのか注意して下さい。

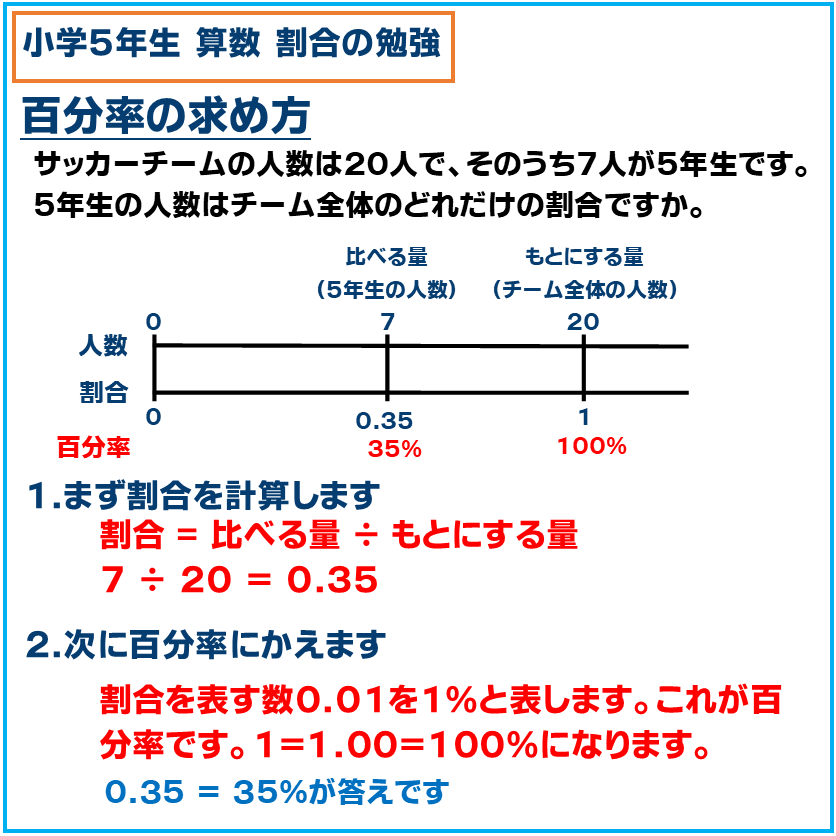
　百分率は割合を〇〇％に変える問題です。まず割合を計算して、上図だと０．３５を出します。そして％で表す場合小数第一位は１０％代の位、小数第二位は１％の位になります。また１は１００％になるのでもし割合が１．３５なら１３５％になります。

　割合を求めてから百分率に変える問題や、逆に百分率を割合に変える問題もあるのでこの辺りは混合しないようによく覚えて下さい。

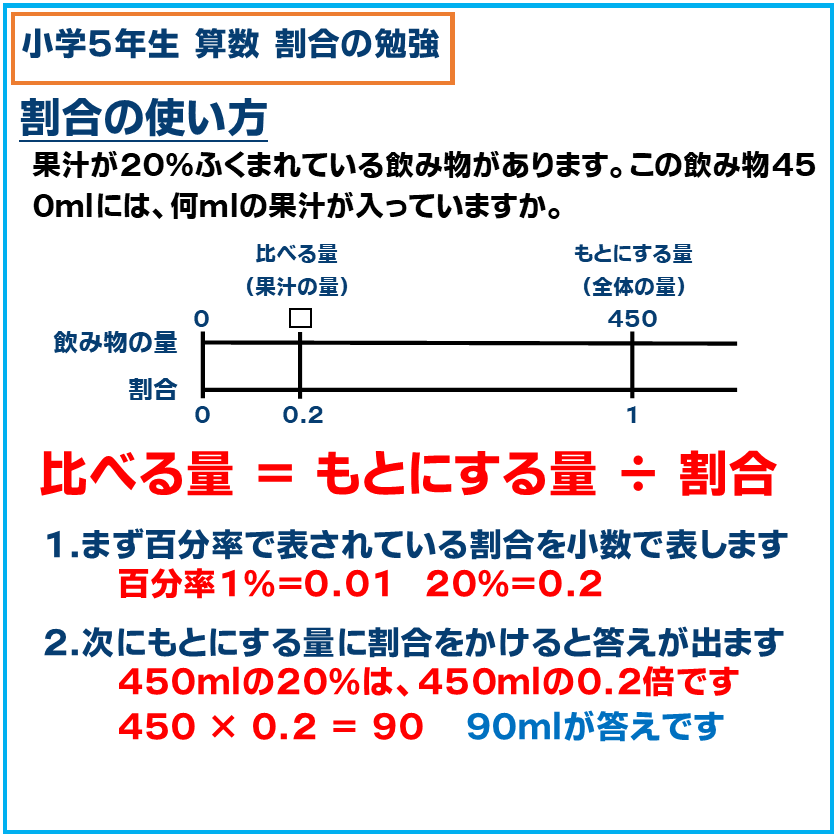
　割合を使ってもとにする量に対する量を計算することができます。上図だと２０％を割合の０．２に変えて、元にする量(全体の量)をかけ算すれば含まれている果汁の量がわかります。

　この辺りから子供達には、問題が複雑に感じるのではないでしょうか。割合と百分率(％)を正しく変えて計算しないと、とんでもない答え(４５０ml　×　２０％　＝　９００など・・・)がノートに書いてあり塾長も頭を抱えることもしばしばです。

　そのような場合は、おそらく今まで習った割合の計算の式を丸暗記しているだけですので、何を何で割るまたはかけるのか文章から読み取れるように何回も教えています。頭の中、またはノートに図を描いてもいいので「もとにする量」と「比べる量」を把握して式を作って、自力で問題が解けるようになるのが理想ですね。

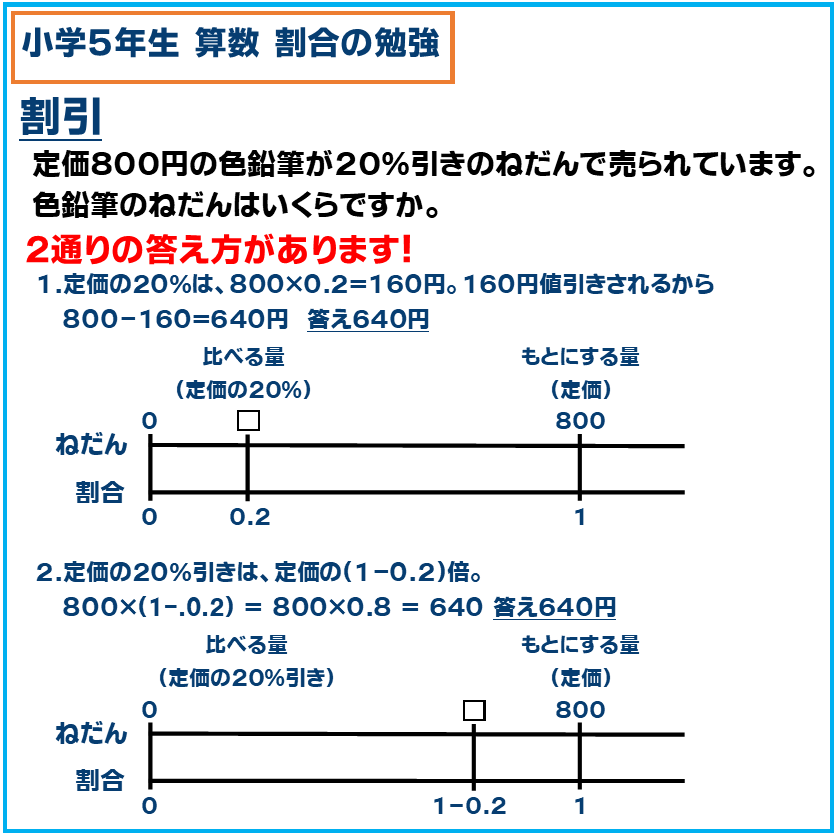
　割合の学習では「値引きの問題」も出題されます。

　値引きの計算方法は２通りあって、１つめは割引される百分率(％)を割合に変えて、定価×割合で値引き額を計算して、定価－値引き額で答えを出す方法です。２つめは１と同様に割合を出して、定価を１と考え(１－割合)×定価で計算します。

　どちらも百分率を一度割合に変えてから計算するので、割合の求め方とその後の計算方法を理解していないと答えが出ません。

　値引きの問題はほぼ文章問題で出題されますので、教科書やドリル等でくり返し復習しないと中々理解できないと思います。

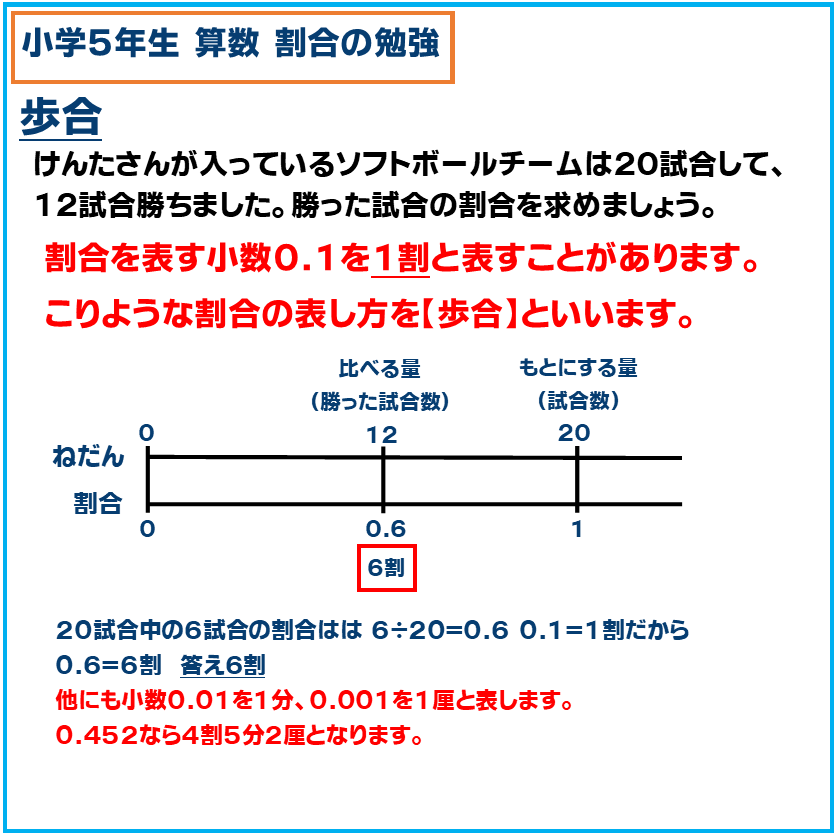
　歩合は割合を百分率とは異なる値で示すことです。

　割合０．１は１割と表します。０．０１は１分、０．００１を１厘と表します。０．４５２なら４割５分２厘となります。百分率なら４５．２％になります。

　こちらは計算より変換を意識して覚えるので比較的簡単です。

　割合の難しいところはただり計算ではなく、何を何でかけるか割るか、また割合↔百分率の変換など今までの計算とは異なり、思考力が問われます。

　こちらでも解き方をくり返し教えていますが、最終的には生徒達が自分の頭でなぜこのように計算するのか理解する必要があります。

　割合は大人になってからでも普段から使っています。今のうちに理解すると中学校での数学も楽になります。

　割合で困っているお子様にはぜひ当塾のわかりやすい体験授業を受けていただくと幸いです。